1. How to convert binary to decimal ?
1. Find the position of every binary digit. We should count the position from the right direction of the number. And the position count starts from 0.
Example
0001 - position of 1 = 0, 0 = 1, 0 = 2, 0 = 3.
2. Multiply every digit with 2 to the power of their corresponding position. (2 position)
3. Finally, calculate the sum of all the multiples.
= 1 x 2 3 + 1 x 2 2 + 1 x 2 1 + 1 x 2 0
= 8 + 4 + 2 + 1
= (15)10
= 1 x 2 3 + 0 x 2 2 + 0 x 2 1 + 1 x 2 0
= 8 + 0 + 0 + 1
= (9)10
2. How to convert binary to octal ?
Group every 3 binary bits from right to left and construct the octal number system.
= (101010101)2
= (101)(010)(101)
= (525)8
= (11111111)2
= (11)(111)(111)
= (377)8
3. How to convert binary to hexadecimal ?
Group every 4 binary bits from right to left and construct the hexadecimal number system.
= (101010101)2
= (1)(0101)(0101)
= (155)16
= (11111111)2
= (1111)(1111)
= (15)(15)
= (ff)16
Converting Decimal Fraction to Binary, Octal, Hexadecimal
A fractional number is a number less than 1. It
may be .5, .00453, .564, etc. We use the multiplication operation to
convert decimal fraction to any other base.
To convert a decimal fraction to—
• binary - multiply by 2
• octal - multiply by 8
• hexadecimal - multiply by 16
Steps for conversion of a decimal fraction to any other base are—
1. Multiply the fractional number with the to Base, to get a resulting number.
2. The resulting number has two parts, non-fractional part and fractional part.
3. Record the non-fractional part of the resulting number.
4. Repeat the above steps at least four times.
5. Write the digits in the non-fractional part starting from upwards to downwards.
Example-1: Convert 0.2345 from Base 10 to Base 2
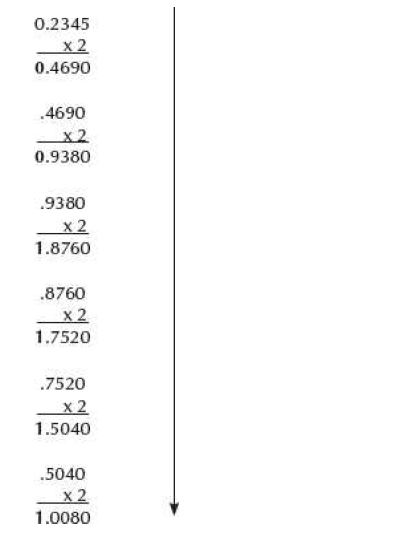
The binary equivalent of (0.2345)10 is (0.001111)2
Example-2: Convert 0.865 from Base 10 to Base 2,8 and 16



0comments:
Post a Comment
Note: only a member of this blog may post a comment.