Complements are used in the digital computers in order to simplify the subtraction operation and for the logical manipulations. For each radix-r system (radix r represents base of number system) there are two types of complements.
| S.N. | Complement | Description |
|---|---|---|
| 1 | Radix Complement | The radix complement is referred to as the r's complement |
| 2 | Diminished Radix Complement | The diminished radix complement is referred to as the (r-1)'s complement |
Binary system complements
As the binary system has base r = 2. So the two types of complements for the binary system are 2's complement and 1's complement.
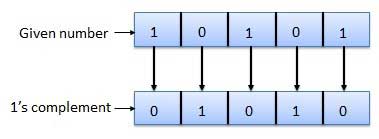
1's complement
The 1's complement of a number is found by changing all 1's to 0's and all 0's to 1's. This is called as taking complement or 1's complement. Example of 1's Complement is as follows.
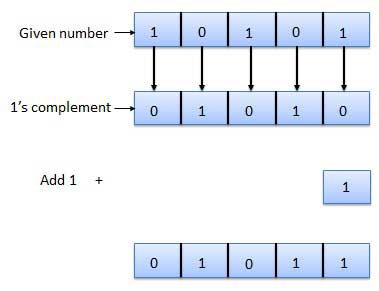
2's complement
The 2's complement of binary number is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.
2's complement = 1's complement + 1
Example of 2's Complement is as follows.
Decimal system complements
In digital logic, decimal complements are employed less frequently than their binary equivalents. The majority of contemporary digital systems rely on binary representations and complements, such as 2's complement, for effective arithmetic operations, even if they still have some historical relevance and few uses.
Below is a summary of the various decimal complements:
1. Ten's complement, or Radix complement:
- found by deducting each number from nine.
- Example: 999 - 375 = 624 is the ten's complement of 375.
2. Nine's Complement, or Diminished Radix Complement:
- found by deducting each number from eight.
- Example: 888 - 375 = 513 is the complement of 375, which equals nine.
3. The Complement of (R-1):
- Reversed each digit from (base - 1) to find.
- For instance, the complement of 375 in (9-1) is equal to 888 - 375 = 513 in decimal notation.
Uses:
- used for subtraction in mechanical calculators in the past.
- utilized in certain applications of some circuits for decimal arithmetic.
- A setting for education in order to comprehend complements.
Restrictions:
- more intricate computations in contrast to binary complements.
- Need more circuits to handle overflows and carry.
- Not effective for big values because to possible overflow of digits.
Decimal vs. Binary Complements:
- Because binary complements—ones and twos—have more uses and are easier to implement, they are utilized more frequently in digital logic.
- With binary complements, representing negative values and carrying out arithmetic operations are more effective.





