Solved Example on Number System Set-I (Decima to Binary, Octal, Hexadecimal conversion)

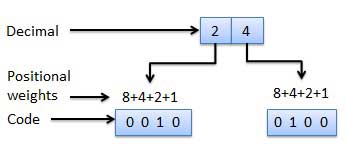
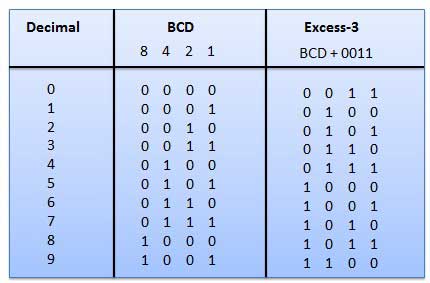
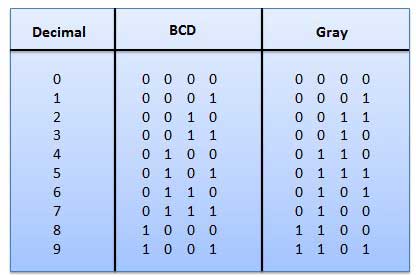
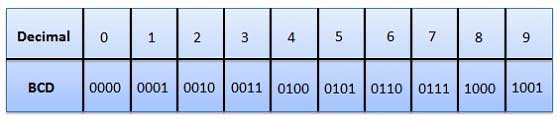
As you know decimal, binary, octal and hexadecimal number systems are positional value number systems. To convert binary, octal and hexadecimal to decimal number, we just need to add the product of each digit with its positional value. Here we are going to learn other conversion among these number systems.

Decimal to Binary

Decimal numbers can be converted to binary by repeated division of the number by 2 while recording the remainder. Let’s take an example to see how this happens.

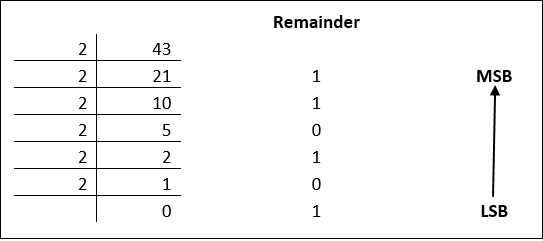
The remainders are to be read from bottom to top to obtain the binary equivalent.

43₁₀ = 101011₂

Decimal to Octal

Decimal numbers can be converted to octal by repeated division of the number by 8 while recording the remainder. Let’s take an example to see how this happens.

Reading the remainders from bottom to top,

473₁₀ = 731₈

Decimal to Hexadecimal

Decimal numbers can be converted to octal by repeated division of the number by 16 while recording the remainder. Let’s take an example to see how this happens.

Reading the remainders from bottom to top we get,

 423₁₀ = 1A7₁₆

 

Here you find step by step process of fractional number conversion to any other number systems. It is very easy to do with some specified steps those are

• We have to multiply the fractional number by base to which number system we want to convert, until the all fractional part is remove/zero.
• Every time we have to take the integer value (before point) after every multiplication, until the all fractional part is remove/zero.
• Then the column of this integer value is read in forward order. That means we have to count those reminder from top to button.

Now take an example to understand the process easily.

Let we have to convert 0.25 decimal numbers to binary number system.

As we discuss above that we have to multiply the fractional number by base to which number system we want to convert. So here we convert the fractional number in binary so we have to multiply by 2.

Now see that process

0.25 x 2 = 0.50   0

0.50 x 2 =1.00     1

See in time of second multiplication the fractional part is remove/zero. So we stop our multiplication and take the column of integer value written in right hand side from top to button.

So equivalent of .2510 is 0.012.

Now if we convert this same number 0.2510 in octal number then we have to multiply with 8.Because the base of octal number is 8.

0.25 x 8 = 2.00        2

So equivalent of .2510 is 0.28.

Now if we convert this same number 0.2510 in Hexadecimal number then we have to multiply with 16.Because the base of octal number is 16.

0.25 x 16 = 4.00 4

So equivalent of .2510 is 0.416.

weighted and unweighted codes

In the coding, when numbers, letters or words are represented by a specific group of symbols, it is said that the number, letter or word is being encoded. The group of symbols is called as a code. The digital data is represented, stored and transmitted as group of binary bits. This group is also called as binary code. The binary code is represented by the number as well as alphanumeric letter.

Advantages of Binary Code

Following is the list of advantages that binary code offers.

• Binary codes are suitable for the computer applications.

• Binary codes are suitable for the digital communications.

• Binary codes make the analysis and designing of digital circuits if we use the binary codes.

• Since only 0 & 1 are being used, implementation becomes easy.

Classification of binary codes

The codes are broadly categorized into following four categories.

• Weighted Codes
• Non-Weighted Codes
• Binary Coded Decimal Code
• Alphanumeric Codes
• Error Detecting Codes
• Error Correcting Codes

Weighted Codes

Weighted binary codes are those binary codes which obey the positional weight principle. Each position of the number represents a specific weight. Several systems of the codes are used to express the decimal digits 0 through 9. In these codes each decimal digit is represented by a group of four bits.

Non-Weighted Codes

In this type of binary codes, the positional weights are not assigned. The examples of non-weighted codes are Excess-3 code and Gray code.

Excess-3 code

The Excess-3 code is also called as XS-3 code. It is non-weighted code used to express decimal numbers. The Excess-3 code words are derived from the 8421 BCD code words adding (0011)₂ or (3)10 to each code word in 8421. The excess-3 codes are obtained as follows −

Example

Gray Code

It is the non-weighted code and it is not arithmetic codes. That means there are no specific weights assigned to the bit position. It has a very special feature that, only one bit will change each time the decimal number is incremented as shown in fig. As only one bit changes at a time, the gray code is called as a unit distance code. The gray code is a cyclic code. Gray code cannot be used for arithmetic operation.

Application of Gray code

• Gray code is popularly used in the shaft position encoders.

• A shaft position encoder produces a code word which represents the angular position of the shaft.

Binary Coded Decimal (BCD) code

In this code each decimal digit is represented by a 4-bit binary number. BCD is a way to express each of the decimal digits with a binary code. In the BCD, with four bits we can represent sixteen numbers (0000 to 1111). But in BCD code only first ten of these are used (0000 to 1001). The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD.

Advantages of BCD Codes

• It is very similar to decimal system.
• We need to remember binary equivalent of decimal numbers 0 to 9 only.

Disadvantages of BCD Codes

• The addition and subtraction of BCD have different rules.

• The BCD arithmetic is little more complicated.

• BCD needs more number of bits than binary to represent the decimal number. So BCD is less efficient than binary.

Alphanumeric codes

A binary digit or bit can represent only two symbols as it has only two states '0' or '1'. But this is not enough for communication between two computers because there we need many more symbols for communication. These symbols are required to represent 26 alphabets with capital and small letters, numbers from 0 to 9, punctuation marks and other symbols.

The alphanumeric codes are the codes that represent numbers and alphabetic characters. Mostly such codes also represent other characters such as symbol and various instructions necessary for conveying information. An alphanumeric code should at least represent 10 digits and 26 letters of alphabet i.e. total 36 items. The following three alphanumeric codes are very commonly used for the data representation.

• American Standard Code for Information Interchange (ASCII).
• Extended Binary Coded Decimal Interchange Code (EBCDIC).
• Five bit Baudot Code.

ASCII code is a 7-bit code whereas EBCDIC is an 8-bit code. ASCII code is more commonly used worldwide while EBCDIC is used primarily in large IBM computers.

Error Codes

There are binary code techniques available to detect and correct data during data transmission.

Error Code	Description
Error Detection and Correction	Error detection and correction code techniques

addition and subtraction of unsigned and signed numbers

The direct method of subtraction taught in elementary schools uses the borrow concept. In this method we borrow a 1 from a higher significant position when the minuend digit is smaller than the corresponding subtrahend digit. This seems to be easiest when people perform subtraction with paper and pencil. When subtraction is implemented with digital hardware, this method is found to be less efficient than the method that uses complements.

The subtraction of two n-digit unsigned numbers M - N (N * 0) in base r can be done as follows:

1. Add the minuend M to the r's complement of the subtrahend N. This performs M + (r' - N) = M - N + r'.

2. If M "" N, the sum will produce an end carry r' which is discarded, and what is left is the result M - N.

3. If M < N, the sum does not produce an end carry and is equal to r' - (N - M), which is the r's complement of (N - M). To obtain the answer in a familiar form, take the r' s complement of the sum and place a negative sign in front.

Consider, for example, the subtraction 72532 - 13250 = 59282. The lO's complement of 13250 is 86750. Therefore:

M = 72532

lO's complement of N = +86750

Sum = 159282

Discard end carry 10' = -100000

Answer = 59282

Now consider an example with M < N. The subtraction 13250 - 72532 produces negative 59282. Using the procedure with complements, we have

M = 13250

lO's complement of N = +27468

Sum = 40718

There is no end carry.

Answer is negative 59282 = 10's complement of 40718

Since we are dealing with unsigned numbers, there is really no way to get an unsigned result for the second example. When working with paper and pencil, we recognize that the answer must be changed to a signed negative number. When subtracting with complements, the negative answer is recognized by the absence of the end carry and the complemented result.

Subtraction with complements is done with binary numbers in a similar manner using the same procedure outlined above. Using the two binary numbers X = 1010100 and Y = 1000011, we perform the subtraction X - Y and Y - X using 2's complemenfs:

X= 1010100

2' s complement of Y = +0111101

Sum = 10010001

Discard end carry 27 = - 10000000

Answer: X - Y = 0010001

y = 1000011

2's complement of X = +0101 100

Sum = 1101111

There is no end carry

Answer is negative 0010001 = 2's complement of 1101111