Signed and Unsigned Binary Numbers

 Understanding Number Representation Techniques

1. Integers can be represented in signed and unsigned ways.
2. Signed numbers use a sign flag to distinguish between positive and negative values.
3. Unsigned numbers store only positive numbers.
4. Techniques include Binary, Octal, Decimal, and Hexadecimal.
5. Binary Number System is a popular technique used in digital systems.
6. Binary System represents binary quantities with two possible states.
7. Binary numbers are indicated by an 0b prefix or a 2 suffix.
8. Unsigned binary numbers lack a sign bit, while signed binary numbers use a sign bit to distinguish between positive and negative numbers.

 1.Sign-Magnitude form

 

Sign-magnitude is one way to represent signed numbers in digital logic. In this form, a fixed number of bits are dedicated to representing the sign and the remaining bits represent the magnitude (absolute value) of the number. Here's a breakdown:

Key points:

• Sign bit: The most significant bit (MSB) is used to represent the sign. 0 indicates positive, and 1 indicates negative.
• Magnitude representation: Remaining bits represent the absolute value of the number, using the same format as unsigned numbers.
• Range: For n bits, the representable range is - (2^(n-1) - 1) to + (2^(n-1) - 1), meaning both positive and negative numbers can be represented within the same format.

Example (8-bit representation):

• +43: 00101011
• -43: 10101011

Limitations:

• Inefficient: Two representations exist for zero (positive 0 and negative 0), wasting space.
• Complex arithmetic: Addition and subtraction require different logic depending on the signs, making them more complex than other methods like 2's complement.
• Overflow detection: Detecting overflow conditions is more challenging compared to other representations.

Comparison with other forms:

• 1's complement: Similar to sign-magnitude but uses an inverted version of the magnitude for negative numbers. Less complex addition/subtraction but suffers from negative zero and overflow issues.
• 2's complement: Adds 1 to the 1's complement representation of negative numbers. Eliminates negative zero, simplifies arithmetic, and offers efficient overflow detection. This is the most common representation in modern digital systems.

Applications:

While not widely used in modern digital logic due to its limitations, sign-magnitude has some historical significance and niche applications:

• Simple educational tool to understand signed number representation.
• Specialized applications where simplicity is valued over efficiency (e.g., low-power systems).

Addition

A number is represented inside a computer with the purpose of performing some calculations using that number. The most basic arithmetic operation in a computer is the addition operation. That’s why a computer can also be called as an adder.

When adding two numbers with the same signs, add the values and keep the common sign. 

Example 1

Add the numbers (+5) and (+3) using a computer. The numbers are assumed to be represented using 4-bit SM notation.

             111  <- carry generated during addition
             0101 <- (+5) First Number
           + 0011 <- (+3) Second Number
             1000 <- (+8) Sum                 

Let’s take another example of two numbers with unlike signs.

Example  2

Add the numbers (-4) and (+2) using a computer. The numbers are assumed to be represented using 4-bit SM notation.

              000 <- carry generated during addition
              1100 <- (-4) First number
           +  0010 <-(+2) Second Number
              1110 <- (-2) Sum

Here, the computer has given the wrong answer of -6 = 1110, instead of giving the correct answer of -2 = 1010.

 

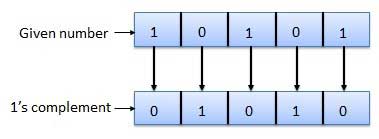
1's Complement

 By inverting each bit of a number, we can obtain the 1's complement of a number. The negative numbers can be represented in the form of 1's complement. In this form, the binary number also has an extra bit for sign representation as a sign-magnitude form.

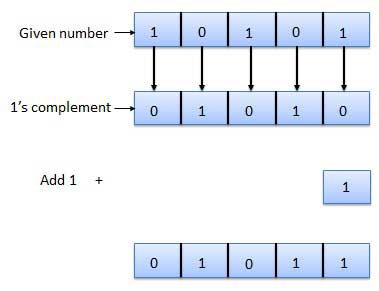
2's Complement

 By inverting each bit of a number and adding plus 1 to its least significant bit, we can obtain the 2's complement of a number. The negative numbers can also be represented in the form of 2's complement. In this form, the binary number also has an extra bit for sign representation as a sign-magnitude form

Complements: r's and (r-1)'s - Radix and Diminished Radix Complements

Complements are used in the digital computers in order to simplify the subtraction operation and for the logical manipulations. For each radix-r system (radix r represents base of number system) there are two types of complements.

S.N.	Complement	Description
1	Radix Complement	The radix complement is referred to as the r's complement
2	Diminished Radix Complement	The diminished radix complement is referred to as the (r-1)'s complement

Binary system complements

As the binary system has base r = 2. So the two types of complements for the binary system are 2's complement and 1's complement.

1's complement

The 1's complement of a number is found by changing all 1's to 0's and all 0's to 1's. This is called as taking complement or 1's complement. Example of 1's Complement is as follows.

2's complement

The 2's complement of binary number is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.

2's complement = 1's complement + 1

Example of 2's Complement is as follows.

 

 

Decimal system complements

 In digital logic, decimal complements are employed less frequently than their binary equivalents. The majority of contemporary digital systems rely on binary representations and complements, such as 2's complement, for effective arithmetic operations, even if they still have some historical relevance and few uses.

Below is a summary of the various decimal complements:

1. Ten's complement, or Radix complement:

•     found by deducting each number from nine.
•     Example: 999 - 375 = 624 is the ten's complement of 375.

2. Nine's Complement, or Diminished Radix Complement:

•     found by deducting each number from eight.
•     Example: 888 - 375 = 513 is the complement of 375, which equals nine.

3. The Complement of (R-1):

•     Reversed each digit from (base - 1) to find.
•     For instance, the complement of 375 in (9-1) is equal to 888 - 375 = 513 in decimal notation.

Uses:

•     used for subtraction in mechanical calculators in the past.
•     utilized in certain applications of some circuits for decimal arithmetic.
•     A setting for education in order to comprehend complements.

Restrictions:

•     more intricate computations in contrast to binary complements.
•     Need more circuits to handle overflows and carry.
•     Not effective for big values because to possible overflow of digits.

Decimal vs. Binary Complements:

•     Because binary complements—ones and twos—have more uses and are easier to implement, they are utilized more frequently in digital logic.
•     With binary complements, representing negative values and carrying out arithmetic operations are more effective.

conversion of numbers from one radix to another radix

We have learned and use the decimal numbering system simply because humans are born with ten fingers! Hence, the numeric system we is the decimal number system, but this system is not convenient for machines since the information is handled codified in the shape of ON or OFF bits.

This means, we have to learn the binary system in addition to the decimal system. We also will discuss the octal and hexadecimal systems because conversion to/from binary is easy and numbers in these systems are easier to read than binary numbers for humans. 

This way of codifying takes us to the necessity of knowing the positional methods of calculation which will allow us to express a number in any base where we need it.

A base of a number system or radix defines the range of values that a digit may have.

Converting numbers from one radix (base) to another is a fundamental concept in computer science and mathematics. Here's an overview of the different methods for conversion:

1. Integer Conversion:

a) Decimal to Another Radix:

1. Divide the number repeatedly by the target radix, noting the remainders from each division (in reverse order). These remainders become the digits in the new base.
2. If the number is negative, convert the absolute value first, then add a negative sign at the end.

Example: Convert 235 (decimal) to binary.

1. 235 / 2 = 117 R 1 -> 1 (least significant digit)
2. 117 / 2 = 58 R 1 -> 1
3. 58 / 2 = 29 R 0 -> 0
4. 29 / 2 = 14 R 1 -> 1
5. 14 / 2 = 7 R 0 -> 0
6. 7 / 2 = 3 R 1 -> 1
7. 3 / 2 = 1 R 1 -> 1
8. 1 / 2 = 0 R 1 -> 1

Therefore, 235 (decimal) = 11101011 (binary).

 

Conversion of decimal number to octal

Now, let's express the same decimal number 1341 in octal notation. 

Conversion of decimal number to hexadecimal

Let's express the same decimal number 1341 in hexadecimal notation. 

The easiest way to convert fixed point numbers to any base is to convert each part separately. We begin by separating the number into its integer and fractional part. The integer part is converted using the remainder method, by using a successive division of the number by the base until a zero is obtained. At each division, the reminder is kept and then the new number in the base r is obtained by reading the remainder from the lat remainder upwards.

b) Another Radix to Decimal:

1. Multiply each digit by its corresponding place value (power of the original radix) and sum the results.

2. Fractional Conversion:

a) Decimal to Another Radix:

1. Multiply the fractional part by the target radix repeatedly. Note the integer part of each product (these become digits in the new base).
2. For the remaining fractional part, repeat step 1 until a repeating pattern emerges or a desired precision is reached.

Example: Convert 0.625 (decimal) to binary.

1. 0.625 * 2 = 1.25 -> 1 (integer part)
2. 0.25 * 2 = 0.5 -> 0 (integer part)
3. 0.5 * 2 = 1.0 -> 1 (integer part)

Therefore, 0.625 (decimal) = 0.101 (binary) (repeating pattern).

b) Another Radix to Decimal:

1. Sum the values of each digit multiplied by its corresponding place value (a fraction of the original radix).

 Example: Convert 234.14 expressed in an octal notation to decimal.